Sonetto的二分讲解

整数二分

1. 确定一个区间，使目标值一定在区间内
2. 找到一个性质，使其满足：
   1)性质具有二段性
   2)答案是二段性的分界点

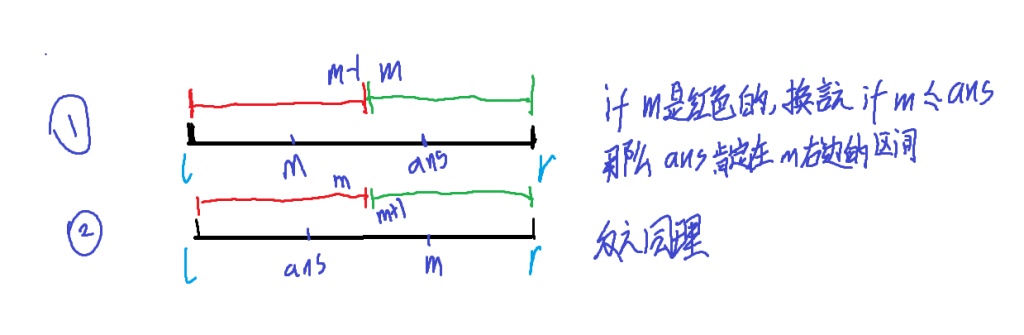
一、 ans 是红色区间的右端点
将[l, r]分成[l, m - 1], [m, r]
如果m是红色的 则 ans 仍在 [m, r]中,
否则 ans 在[l, m-1]中。

while(l < r){
m = (l + r + 1) / 2;
if(m <= ans)
l = m;
else
r = m - 1;
}

二、 ans 是绿色区间的左端点
将[l, r]分成[l, m ], [m+1, r]
如果m是绿色的 则 ans 仍在 [l, m]中,
否则 ans 在[m + 1, r]中.

while(l < r){
m = (l + r) / 2; if(m >= ans)
r = m;
else
l = m + 1;
}

实数二分

和整数二分的差别只是不需要考虑边界问题
条件改为while(r - 1 > 1e-x)
x为一个符合题意的数，最好比题目给的精度大二左右

另一种更容易理解的整数二分
在这个方法中l和r永远不可能相等
a[l] 始终 < x a[r] 始终 >= x
所以找答案只需要判断a[r]是否等于目标值

while(l + 1 != r){
int mid = (l + r) >> 1;
if(check()) l = mid;
else r = mid;
}
if(a[r] == x) cout << r << ' ';
else cout << -1 << ' ';